The Lobster Programming Language

Lobster is a game programming language. Unlike other game making systems that focus on an engine/editor that happens to be able to call out to a scripting language, Lobster is a general purpose stand-alone programming language that comes with a built-in library suitable for making games and other graphical things. It is therefore not very suitable for non-programmers.

It’s also meant to be portable (mostly courtesy of OpenGL/SDL/Freetype), allowing your games to be run on Windows, Mac OS X, iOS, Linux, and Android (in that order of maturity, currently).

Lobster is Open Source (ZLIB license) and can be found on github. Online copy of the full documentation. Discuss things in the google+ community or like the Facebook page.

Features

Features have been picked for their suitability in a game programming language, and in particular to make code terse, quick to write and refactor. It is meant to not hold you back to get an idea going quickly. It is quite the opposite of a robust enterprise language.

  • Language
    • Static Typing that still feels like a Dynamically Typed Language thanks to Flow-Sensitive Type-Inference and Specialization.
    • Python-style indentation based syntax with C-style flavoring
    • Lightweight Blocks / Anonymous Functions that make any function using them look identical to built-in control structures
    • Lexically Scoped with optional Dynamic Scoping
    • Vector operations (for math and many other builtins)
    • Multimethods (dynamic dispatch on multiple arguments at once)
    • First Class Stackful Asymmetric Coroutines
    • Optionally immutable objects
  • Implementation
    • Choose between using the convenient bytecode VM, or compilation to C++ for extra speed.
    • Reference Counting with cycle detection at exit, or optional garbage collection calls
    • Debugging functionality (stack traces with full variable output)
    • Dynamic code loading
    • Relatively fast (several times faster than Python/Ruby, about as fast as non-JIT Lua) and economical (low overhead memory allocation)
    • Easy to deploy (engine/interpreter exe + compressed bytecode file)
    • Modularly extendable with your own library of C++ functions
  • Engine
    • High level interface to OpenGL functionality, very quick to get going with simple 2D geometric primitives
    • 3D primitive construction either directly from triangles, or using high level primitives made into meshes through marching cubes
    • GLSL shaders (usable accross OpenGL & OpenGL ES 2 without changes)
    • Accurate text rendering through FreeType
    • Uniform input system for mouse & touch
    • Simple sound system supporting .wav and .sfxr synth files.
    • Comes with useful libraries written in Lobster for things like A* path finding and game GUIs

Examples

let’s start with syntax and blocks:

def find(xs, fun):
    for(xs) x, i:
        if fun(x):
            return i
    return -1

var r = 2
var i = find [ 1, 2, 3 ]: _ > r

We can learn a lot about the language from this tiny example:

  • find is a function that takes a vector and a function as argument, and returns the index of the first element for which that function returns true, or -1 if none.
  • It uses an indentation based syntax, though in this example the for-if-return could also have been written on a single line.
  • Blocks / anonymous function arguments are always written directly after the call they are part of, and generally have the syntax of a (possibly empty) list of arguments (separated by commas), separated from the body by a :. The body may either follow directly, or start a new indentation block on the next line. Additionally, if you don’t feel like declaring arguments, you may use variable names starting with an _ inside the body that are automatically declared.
  • for and if look like language features, but they have no special syntactical status compared to find. Any such functions you add will work with the same syntax.
  • Notice the complete lack of type declarations. The code is fully statically typed, however, type inference is smart enough to assign types to everything, and functions like find get specialized to work on whatever arguments they are called with, in this case a list of ints, and a specific lambda. Specialization not only increases the range of code type inference can handle, it allows the compiler to optimize this particular case as if you had hard-coded the loop (much like C++ templates).
  • blocks/functions may refer to “free variables”, i.e. variables declared outside of their own scope, like r. This is essential to utilize the full potential of blocks.
  • i will contain 2 at the end of this (the index of element 3). It does not clash with the other i because of lexical scoping. Here = means assignment, and var defines a new variable (you can also use : as a shorthand for var and = together).
  • return returns from find, not from the enclosing function (which would be the block passed to if). In fact, it can be made to return from any named function, which makes it powerful enough to implement exception handling in Lobster code, instead of part of the language.
  • Not only are higher order functions like find easy to write and use, you can convert any such functions into coroutines trivially, e.g. coroutine for(10) creates a coroutine object that yields values 0..9 on demand. Because in lobster coroutines and higher order functions are written in the same way (there is no yield keyword), they are more composable and interchangable.

Types, multimethods, immutables and vector ops:

value point { x, y }
value circle : point { radius }
value ray : point { dir }

def intersect(p:point, c:circle): magnitude(p - c) < c.radius
def intersect(r:ray, c:circle): ...
def intersect(c1:circle, c2:circle): ...
...

assert intersect(point { 1, 1 }, circle { 2, 2, 2 })

What we learn here:

  • we can declare custom datatypes, that can optionally inherit from existing datatypes
  • we can declare them with either value or struct, where the former means the object is immutable: its fields may not be assigned to after construction. This enforces more functional style programming for objects which can be seen as unit things (like points and vectors).
  • objects are very much like the typed version of the generic vectors we saw earlier, and are treated similarly by the language in many ways (e.g. vector operations also work on them)
  • We can declare multiple version of a function, and the language will pick dynamically which one to run, based on all arguments (most OO languages only use the first argument for this, thus writing a function like intersect requires double dispatch, i.e. 2 levels of methods). If two functions apply to a certain set of arguments, the most specific one (starting from the first argument) is picked. If such an ordering can’t be determined at compile time, that is a compile time error. If no functions apply at runtime, that’s a runtime error (which you can avoid with a catch-all default function version with no types).
  • we can specify types for arguments with :, also for single functions. Besides their use in multimethods, they can be used in regular functions to make compile time type errors simpler. You can even specify the type with ::, which allows you direct access to all members of the type, so you can write x instead of p.x etc.

Enough of dry programming language stuff, how do we draw?

include "vec.lobster"
include "color.lobster"

const directions = [ xy_0, xy_x, xy_y ]

def sierpinski(depth):
    if depth:
        gl_scale 0.5:
            for(directions) d:
                gl_translate d:
                    sierpinski(depth - 1)
    else:
        gl_polygon(directions)

fatal(gl_window("sierpinski", 512, 512))

while gl_frame():
    if gl_wentdown("escape"): return
    gl_clear(color_black)
    gl_scale(float(gl_windowsize()))
    sierpinski(7)

which produces:

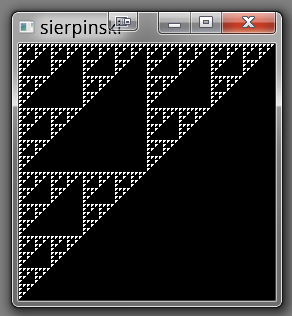
What do we see:

  • if we skip to gl_window, this creates the window and sets up OpenGL basics. This can theoretically fail which will return us an error string, but here for the example we’re lazy.
  • rendering in Lobster centers around frames like in most game engines, so we redraw everything every time (this example has no animation or interaction, so that looks a bit silly). gl_frame takes care not only of frame swapping, but updating input etc as well
  • gl_scalevec allows us to scale all rendering by specifying the unit size (compared to the previous scale, which by default is pixel size). Using the current window size thus gets us a canvas with a resolution of 1.0 x 1.0 which is convenient for the algorithm we’re about to run
  • The include pulls in definitions for 2d/3d/4d vectors and some useful constants (e.g. vec_0 is a vector of all zeroes).
  • The recursive function then keeps subdividing and scaling in 3 directions until it gets to the bottom of the recursion where it draws the triangles

To see more about the builtin functionality of Lobster (graphics or otherwise), check out the builtin functions reference (this particular file may be out of date, it can be regenerated by the running lobster -r). You can also check out draft version of the full Lobster documentation, in particular the Language Reference.

Most recent version of everything is on GitHub.

Lobster examples on Rosetta Code.

Feel like discussing Lobster? There’s a Google+ community for it, and Facebook page.

And for fun here’s a Minecraft clone in lobster whose code fits inside a single screenshot.

And finally, as an example of the extreme economy of code you can get to using the compositionality of higher order functions judiciously, the code below implements the A* algorithm for any kind of search, with specialized versions for nodes in 2D/3D/nD space, 2D grids, and GOAP (goal oriented action planning) all in a tiny amount of code, with no code duplication. Yes, readability suffers, but if you’ve ever implemented these algorithms (including GOAP), you probably realize this is quite an extreme level of factoring:

// A* search functionality

include "std.lobster"
include "vec.lobster"

struct astar_node {
    G:float = 0.0,
    H:float = 0.0,
    F:float = 0.0,
    previous = nil,
    state,
    delta = nil,
    open:int = false,
    closed:int = false
}

def astar_clear(n::astar_node):
    open = closed = false
    previous = nil

// the generic version searches any kind of graph in any kind of search space,
// use specialized versions below

def astar_generic(startnode, endcondition, generatenewstates, heuristic):
    openlist := [ startnode ]
    n := startnode or nil
    while n and !endcondition(n):
        openlist.removeobj(n)
        n.closed = true
        generatenewstates(n) delta, cost, nn:
            if !nn.closed:
                G := n.G + cost
                if ((!nn.open and openlist.push(nn)) or G < nn.G):
                    nn.open = true
                    nn.delta = delta
                    nn.previous = n
                    nn.H = heuristic(nn.state)
                    nn.G = G
                    nn.F = G + nn.H
        n = nil
        for(openlist) c:
            if !n or c.F < n.F or (c.F == n.F and c.H < n.H):
                n = c
    path := []
    while n:
        path.push(n)
        n = n.previous
    path

// specialized to a graph in 2D or 3D space (assumes pre existing nodes), usage:
// - create a graph out of nodes inherited from astar_node above
// - costf must compute the cost of traversal between 2 nodes, 0 for impassable
// - neighbors generates adjacent nodes
// - returns a list of nodes from end to start inclusive, or empty list if no path

def astar_graph(startnode, endnode, costf, distancef, neighbors):
    astar_generic(startnode) n:
        n == endnode
    generatenewstates n, f:
        neighbors(n) nn:
            cost := costf(n, nn)
            if cost > 0:
                f(nn.state - n.state, cost, nn)
    heuristic state:
        distancef(state - endnode.state)

// specialized to a 2D grid (specialized case of a graph)

def astar_2dgrid(isocta, gridsize, startnode, endnode, getnode, costf):
    directions := cardinal_directions
    def astar_distance(distancef):
        astar_graph(startnode, endnode, costf, distancef) n, f:
            for(directions) delta:
                np := n.state + delta
                if np.inrange(gridsize):
                    f(getnode(np))
    if isocta:
        directions = append(directions, diagonal_directions)
        astar_distance() v:
            x := abs(v.x)
            y := abs(v.y)
            big := max(x, y)
            small := min(x, y)
            sqrt(2) * small + big - small
    else:
        astar_distance() v:
            abs(v.x) + abs(v.y)

// specialized to do GOAP (nodes created on the fly)

def goapf(state:[int]) :== int

value goapaction {
    name:string,
    precondition:goapf,
    effect:goapf
}

struct goap_node = astar_node(goap_node?, [int], goapaction?)

def astar_goap(goapactions:[goapaction], initstate:[int], heuristic, endcondition):
    H := heuristic(initstate)
    existingnodes := [ goap_node { H: H, F: H, state: initstate } ]
    astar_generic(existingnodes[0]):
        endcondition(_.state)
    generatenewstates n, f:
        for(goapactions) act:
            pre := act.precondition
            if pre(n.state):
                nstate := n.state.copy
                eff := act.effect
                eff(nstate)
                i := existingnodes.find(): equal(_.state, nstate)
                nn := i >= 0 and existingnodes[i] or goap_node { nstate }
                f(act, 1, nn)
    heuristic: heuristic(_)

Also note that while the structs contain some types, the functions contain very little of them, showing the power of the type inference algorithm.

Probably not the best example to sell a language.. it is possible to write simple looking code in it too, honest :)